Призма правильной четырехугольной формы, также известная как куб, является простым и уникальным телом в геометрии. Изучение ее свойств позволяет получить глубокое понимание и использовать его в различных задачах. Площадь диагонального сечения призмы является важным параметром, который можно рассчитать с помощью нескольких простых шагов.
Для определения площади диагонального сечения призмы правильной четырехугольной формы нужно знать длину ребра и длину диагонали одной из граней призмы.
Чтобы найти площадь диагонального сечения, умножьте длину ребра на длину диагонали грани. Ответ будет в квадратных единицах измерения.
Как найти площадь диагонального сечения призмы
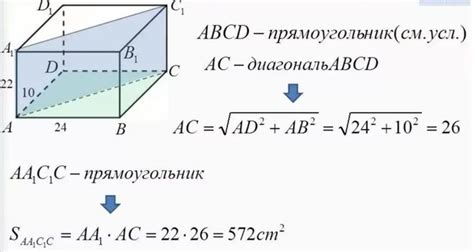
Для этого нужно знать форму грани и длину ее диагонали.
Следующие шаги помогут вам найти площадь диагонального сечения призмы:
- Определите форму основания призмы.
- На основе формы основания определите способ вычисления площади.
- Определите длину диагонали сечения призмы.
- Используя найденные значения, вычислите площадь диагонального сечения призмы.
Например, для прямоугольной призмы площадь диагонального сечения можно найти как произведение длины прямоугольника и длины его диагонали.
Для правильной четырехугольной призмы все стороны и углы основания равны между собой. Площадь диагонального сечения можно найти как произведение длины стороны основания и длины его диагонали.
Теперь, когда вы знаете, как найти площадь диагонального сечения призмы, вы можете легко решать задачи, связанные с этой темой!
Определение исследуемой фигуры
При изучении площади диагонального сечения призмы правильной четырехугольной следует понимать, что это особая форма призмы, имеющая четырехугольную основу и боковые грани, состоящие из треугольников. Площадь диагонального сечения определяется как площадь плоскости, образованной пересечением боковых граней призмы с плоскостью, проходящей через ее диагональ.
Для рассчета площади диагонального сечения призмы нужно знать размеры основания и высоту призмы. Основание четырехугольной призмы может быть прямоугольником, ромбом или другой четырехугольной фигурой с равными сторонами. Высота призмы определяется как расстояние между основаниями и соединяет их вершины.
Изучение и расчет площади диагонального сечения правильной четырехугольной призмы является важным этапом в геометрии и строительстве, позволяющим определить объемы, площади поверхностей и другие характеристики данной геометрической фигуры.
Методы расчета площади диагонального сечения
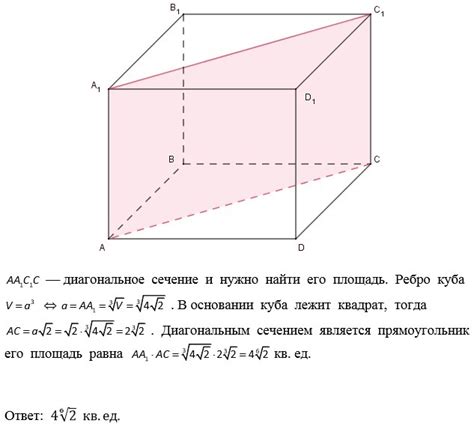
Метод разложения на треугольники. Этот метод основан на представлении диагонального сечения в виде двух наклонных треугольников. Для вычисления площади каждого треугольника необходимо найти длину его основания и высоту. Затем площади обоих треугольников суммируются.
Метод использования геометрических формул. Этот метод предполагает использование различных геометрических формул для вычисления площади диагонального сечения призмы.
Метод интеграла. Этот метод основан на применении интеграла для вычисления площади диагонального сечения призмы. Однако он требует специальных математических знаний и может быть сложен для понимания и применения.
В зависимости от конкретной задачи и доступных данных, можно использовать один из перечисленных методов или комбинацию нескольких. Важно учитывать, что вычисление площади диагонального сечения призмы правильной четырехугольной является сложной задачей, которая требует точных математических расчетов.