Математика содержит разнообразные функции, и важно знать, возрастает ли функция или убывает. Эти сведения помогут понять поведение функции, найти точки максимума и минимума, проанализировать график и решить различные математические задачи.
Основные принципы определения возрастания и убывания функции сводятся к следующему: если функция увеличивается при увеличении аргумента, она называется возрастающей, а если уменьшается - убывающей.
Чтобы точно определить, возрастает ли функция или убывает, нужно проанализировать ее производную. Если производная положительна, функция возрастает, если отрицательна - убывает.
Понятие функции

Функция может быть представлена графически с помощью графика функции, на котором отображаются все точки, соответствующие паре (аргумент, значение функции). График функции может быть обычной линией, кривой или иметь другой геометрический вид.
Функции могут быть возрастающими или убывающими, в зависимости от того, как меняются значения функции с увеличением аргумента. Если значения функции увеличиваются при увеличении аргумента, то говорят, что функция возрастает. Если значения функции убывают при увеличении аргумента, то говорят, что функция убывает.
Для определения возрастания или убывания функции нужно анализировать изменение наклона ее графика. Положительный наклон соответствует возрастанию функции, отрицательный - убыванию, а нулевой наклон указывает на наличие экстремума.
Определение возрастания и убывания

Для определения поведения функции на определенном промежутке нужно анализировать ее и использовать математические методы.
Шаг 1: Вычисление разности функции
Начнем с вычисления разности функции на рассматриваемом промежутке. Выберем две точки на промежутке и найдем их функциональные значения. Затем вычислим разность между этими значениями. Если разность положительна, то функция возрастает. Если разность отрицательна, то функция убывает.
Шаг 2: Проверка увеличения и убывания
Для подтверждения возрастания или убывания функции необходимо проверить значения разности функции для всех точек на промежутке. Если разность положительна для всех точек, то функция возрастает. Если разность отрицательна для всех точек, то функция убывает.
Шаг 3: Анализ производной функции
Если производная функции положительна на промежутке, то функция возрастает. Если производная функции отрицательна на промежутке, то функция убывает. Если производная функции равна нулю, то функция может иметь точки экстремума.
Методы выше позволяют точно определить, является ли функция возрастающей или убывающей на промежутке.
Возрастание функции
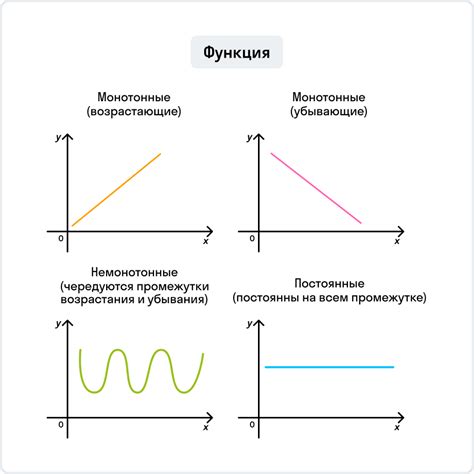
Функция считается возрастающей на интервале, если выполняется условие:
f(x1) < f(x2)
Для любых двух точек x1 и x2 из данного интервала, при условии, что x1 < x2. Таким образом, значение функции возрастает, когда аргумент увеличивается.
Для определения возрастания функции, можно также использовать производную. Если производная функции положительна на интервале, то функция возрастает на нем. Производная функции показывает скорость изменения функции в каждой ее точке.
Например, функция f(x) = 2x + 1 возрастает на всей числовой прямой, так как производная этой функции равна 2, что является положительным числом.
Убывание функции
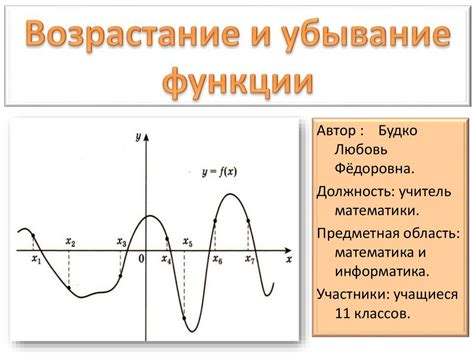
Функция называется убывающей, если для любых двух точек на ее графике, расположенных слева направо, значение функции в первой точке больше значения функции во второй точке.
Если значение функции уменьшается при увеличении аргумента, то функция является убывающей.
График убывающей функции движется сверху вниз - функция опускается по вертикальной оси при движении вправо по горизонтальной оси.
Для определения убывания функции, сравнивают значения функции в разных точках. Если значение в первой точке больше, чем во второй, функция убывает.
Например, функция y = -x убывающая, так как при увеличении x, уменьшается y. График - прямая линия из верхнего левого угла в нижний правый.
Важно учитывать, что функция может быть убывающей только на определенном интервале значений аргумента, например, на отрезке [a, b]. За пределами этого интервала функция может быть возрастающей или иметь другое поведение.
Определение функции 9 класс
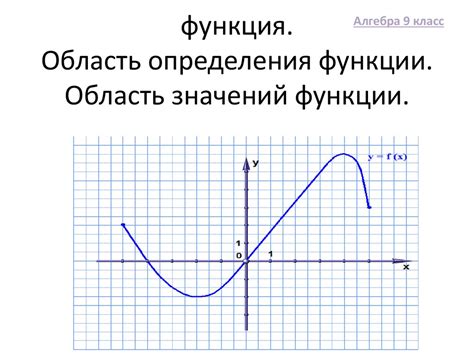
Для начала, следует определить область определения функции. Область определения - это множество значений аргумента функции, при которых функция имеет смысл. При решении задач, связанных с определением возрастания или убывания функции, область определения обычно считается интервалом.
Затем, следует проанализировать производную функции. Производная - это функция, показывающая скорость изменения значения исходной функции в каждой ее точке. Если производная положительна на интервале, то функция возрастает на этом интервале. Если производная отрицательна на интервале, то функция убывает на этом интервале. Если производная равна нулю на интервале, то функция имеет экстремум на этом интервале.
Экстремум может быть и точкой максимума, и точкой минимума функции. Для того чтобы определить, является ли точка экстремумом, следует проанализировать знаки производных слева и справа от этой точки. Если знак производной меняется (например, с плюса на минус), то точка будет точкой экстремума. Если знак производной не меняется (например, плюс плюс), то точка будет точкой перегиба.
Определение возрастания или убывания функции в 9 классе сводится к анализу области определения, производной и экстремумов. Этот процесс помогает понять поведение функции и решать связанные задачи.
Математическое определение функции 9 класс

Функция может быть задана алгоритмическим описанием, графиком или формулой. В 9 классе чаще всего рассматривается функция, заданная алгоритмическим описанием или формулой.
Функция может быть возрастающей или убывающей. Возрастающая функция означает, что с увеличением значения аргумента, значения функции также увеличиваются. Убывающая функция, наоборот, означает, что с увеличением значения аргумента, значения функции уменьшаются.
Функция возрастает, если ее производная положительна, и убывает, если производная отрицательна. Для определения этого нужно найти производную функции и проанализировать ее знак.
| Функция | Производная | Знак производной | Возрастание/убывание |
|---|---|---|---|
| f(x) | f'(x) | + | Возрастает |
| g(x) | g'(x) | - | Убывает |
Графическое определение функции 9 класс
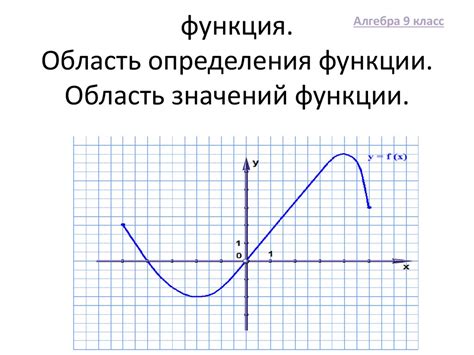
Для определения возрастания или убывания функции на графике, нужно изучить, как меняются ее значения при изменении аргумента.
Если при увеличении аргумента значения функции становятся все больше, то она возрастает. График будет расти.
Если при увеличении аргумента значения функции становятся все меньше, то она убывает. График убывает.
Важно понимать, что чтобы определить возрастание или убывание функции, нужно анализировать ее изменение между значениями аргумента, на которых функция определена.
Например, если график функции - прямая линия, то функция будет возрастать на всей области определения.
График позволяет визуально определить изменение функции при изменении аргумента и определить ее возрастание или убывание без использования аналитических методов.
Как определить возрастание функции 9 класс
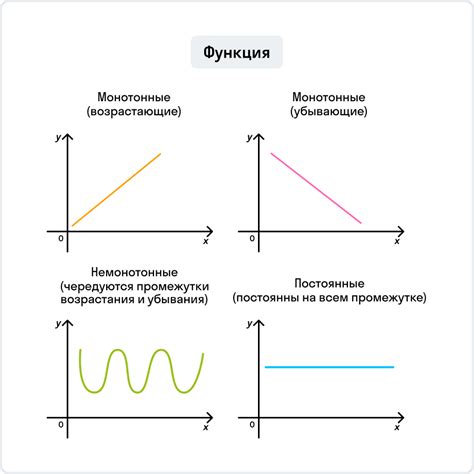
Для определения возрастания функции можно использовать следующие методы:
- Исследовать производную функции. Если производная положительна на некотором промежутке, то функция возрастает на этом промежутке.
- Проверить знаки функции на разных участках графика. Если функция положительна на некотором промежутке, то она возрастает на этом промежутке.
- Оценить приращение функции. Если значение функции прирастает при увеличении аргумента, то функция возрастает.
Важно помнить, что данные методы работают только для непрерывных функций на заданном промежутке. Поэтому перед исследованием возрастания функции необходимо убедиться в непрерывности функции и её производной.
Примечание: Для более подробного изучения темы "возрастание функции" рекомендуется обратиться к учебнику по математике для 9 класса или проконсультироваться с учителем.
Как определить убывание функции 9 класс
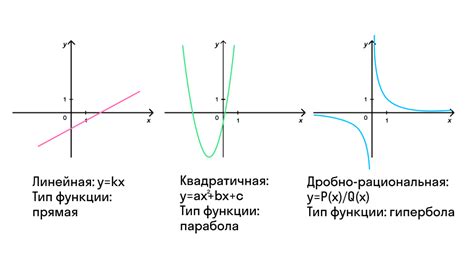
Убывание функции в математике означает, что значения функции уменьшаются по мере увеличения аргумента. Для определения убывания функции необходимо проанализировать ее производную.
1. Первым шагом необходимо найти производную функции. Производная функции показывает, как меняется функция относительно аргумента. Если производная положительна, то функция возрастает, если отрицательна - функция убывает.
2. Найдите производную и решите неравенство f'(x) < 0. Если решение существует, то функция убывает.
3. При решении неравенства важно учитывать область определения функции и ее график. Если функция не определена или постоянна, то она не убывает.
4. Если производная равна нулю или не существует, это может указывать на экстремумы функции. Требуется детальный анализ.
Пример:
Рассмотрим функцию f(x) = x^2 - 3x + 2. Найдем производную: f'(x) = 2x - 3.
Так как f'(x) = 2x - 3 < 0 при x < 3/2, то функция убывает на (-∞, 3/2).
Для определения убывания функции используйте анализ производной, решение неравенств, область определения функции и график.