Равносторонний треугольник - это треугольник, у которого все три стороны равны. Он является одним из самых особенных и интересных геометрических объектов. Высота равностороннего треугольника перпендикулярна одной из его сторон и проходит через противоположный угол. Она делит треугольник на два равных неправильных треугольника и является линией симметрии треугольника.
В равностороннем треугольнике высоту можно найти с помощью формулы: Высота = (сторона * √3) / 2
Например, если сторона равностороннего треугольника равна 6, то его высота будет 3√3.
Используя эту формулу, можно легко вычислить высоту треугольника, зная длину его стороны.
Определение равностороннего треугольника

В равностороннем треугольнике все углы равны между собой и составляют по 60 градусов каждый.
Равносторонний треугольник имеет все стороны одинаковой длины и углы в 60 градусов.
| Свойство | Описание |
|---|---|
| Все стороны равны | В равностороннем треугольнике все стороны имеют одинаковую длину. |
| Все углы равны | Углы равностороннего треугольника равны 60 градусам каждый. |
Равносторонние треугольники имеют особенности, которые могут быть использованы для решения различных задач, таких как нахождение высоты треугольника.
Теорема Пифагора для равностороннего треугольника
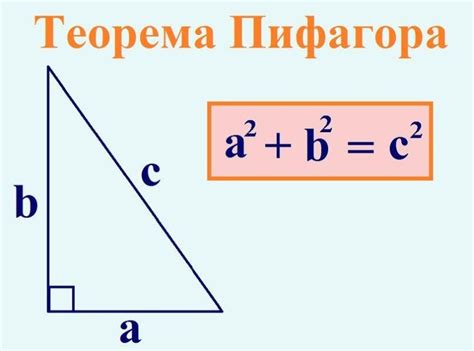
В равностороннем треугольнике также можно использовать теорему Пифагора с небольшими изменениями. Треугольник состоит из трех равносторонних маленьких треугольников.
Один из этих маленьких треугольников имеет две равные стороны и третью сторону в качестве основания. Это создает прямоугольный треугольник, где можно применить теорему Пифагора.
Так как обратное применение теоремы Пифагора невозможно, для определения высоты в равностороннем треугольнике необходимо использовать другие методы, такие как свойства равностороннего треугольника и смежные углы.
Теорема Пифагора может быть применена во многих геометрических фигурах, включая равносторонний треугольник. Эти математические свойства помогают углубить понимание фигур и решать задачи.
Способ 1: Вычисление высоты

Высота равностороннего треугольника может быть легко вычислена с использованием формулы, зависящей от длины стороны треугольника.
Формула для вычисления высоты равностороннего треугольника: h = (корень из 3 * a) / 2, где h - высота, a - длина стороны.
Для примера, предположим, что длина стороны равностороннего треугольника равна 6 единицам. Чтобы найти высоту, мы можем использовать формулу:
h = (корень из 3 * 6) / 2
h = (1.732 * 6) / 2
h = 10.392 / 2
h = 5.196
Таким образом, высота равностороннего треугольника со стороной длиной 6 единиц равна 5.196 единицам.
Способ 2: Создание перпендикуляра к стороне треугольника
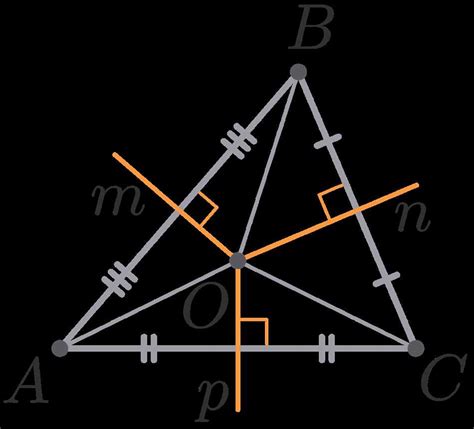
1. Выберите одну из сторон треугольника и выберите произвольную точку на этой стороне.
2. Используя циркуль или компас, отметьте два одинаковых радиуса из выбранной точки. Эти радиусы должны быть достаточно длинными, чтобы они пересекали обе другие стороны треугольника.
3. Соедините точки пересечения радиусов с противоположными вершинами треугольника, образуя два отрезка.
4. Используя циркуль или компас, отметьте точку пересечения этих двух отрезков. Это будет вершина перпендикуляра, опущенного из выбранной точки на сторону треугольника.
5. Проведите прямую линию, проходящую через эту вершину перпендикуляра и середину противолежащей стороны треугольника. Эта линия будет являться высотой треугольника.
Этот метод основан на свойствах равносторонних треугольников и перпендикуляров. Он позволяет точно определить высоту треугольника без использования формул или сложных вычислений.
Способ 3: Применение теоремы косинусов
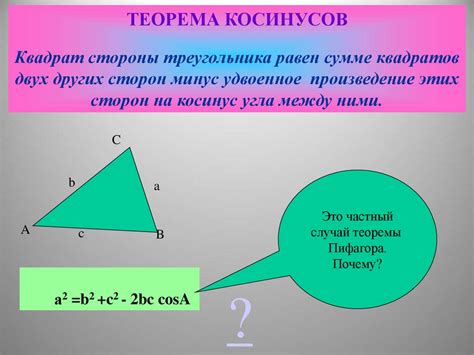
Для равностороннего треугольника все стороны равны, поэтому формула для нахождения высоты упрощается:
h² = (a² * 2) / 3
где h - высота, a - длина стороны треугольника.
Для решения этой формулы необходимо знать длину стороны равностороннего треугольника.
Теорема косинусов поможет найти высоту в данном треугольнике, используя известную длину стороны. Это может пригодиться при решении геометрических задач или при вычислении площади треугольника.
Когда требуется использовать высоту в равностороннем треугольнике

Использование высоты в равностороннем треугольнике может быть полезным в различных задачах:
- Вычисление площади: Высота является одним из способов вычисления площади равностороннего треугольника. Площадь равностороннего треугольника равна половине произведения длины любой стороны на соответствующую ей высоту.
- Вычисление длины: Высота может быть использована для вычисления длины других отрезков в равностороннем треугольнике. Например, длина высоты, опущенной из вершины, равна половине произведения длины любой стороны на корень из трех.
- Определение центра масс: Высота является медианой треугольника, проходящей через вершину. Она пересекается с двумя другими медианами, и точка пересечения всех трех медиан является центром масс равностороннего треугольника.
- Определение взаимного расположения: Высота может использоваться для определения взаимного расположения треугольников. Если высоты равностороннего треугольника пересекаются внутри каждого из трех других треугольников, то треугольники называются перспективными, а точка пересечения высот называется точкой перспективы.
Высота в равностороннем треугольнике имеет много важных применений и может быть использована для решения различных задач, связанных с геометрией и расчетами.
Примеры использования высоты
Высота равностороннего треугольника имеет ряд практических применений. Ниже приведены несколько примеров использования высоты:
- Вычисление площади треугольника: Высота является одной из основных составляющих формулы для вычисления площади равностороннего треугольника.
- Научные и инженерные расчеты: В различных областях науки и инженерии, знание высоты треугольника может быть важно для проведения расчетов или определения параметров объектов или систем.
- Геометрические построения: Высота треугольника используется при проведении различных геометрических построений, например, при построении перпендикуляра к стороне треугольника через заданную точку.
- Архитектурное проектирование: Высота треугольника может быть использована как важный параметр при проектировании архитектурных объектов, таких как пирамиды или шпили зданий.
Высота равностороннего треугольника имеет множество применений в различных областях, от математики и геометрии до архитектуры и инженерии.
Дополнительные сведения о равностороннем треугольнике
| Сторона | Длина высоты |
| А | h = (√3/2) * a |
| A | h = (√3/2) * A |
| Б | h = (√3/2) * Б |
Где a - длина стороны равностороннего треугольника, h - длина высоты. Отношение между длиной стороны и высотой равностороннего треугольника всегда равно √3/2.
Равносторонний треугольник имеет особенность: центр окружности, описанной около него, совпадает с его центром. Радиус этой окружности равен отрезку от центра треугольника до любой его вершины - такой треугольник называется описанным.
Высоту в равностороннем треугольнике можно найти различными способами, включая использование формулы для расчета площади треугольника или теоремы Пифагора.
Для нахождения высоты равностороннего треугольника можно воспользоваться формулой площади: S = (a^2 * sqrt(3))/4, где a - длина стороны. Высота будет равна h = (2 * S)/a.
Также можно использовать теорему Пифагора: h = (a * sqrt(3))/2, для треугольника со стороной a.
Таким образом, высоту равностороннего треугольника можно найти различными способами, например, используя формулу площади или теорему Пифагора.