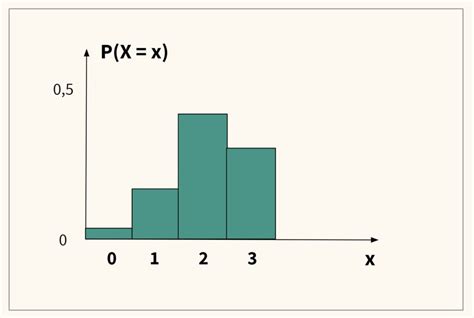
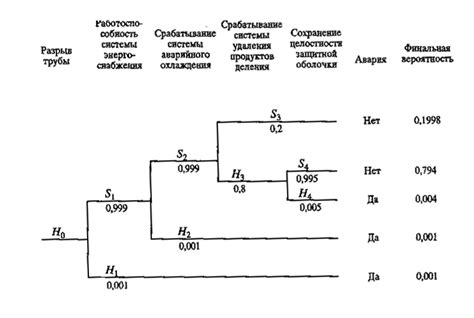
Биномиальное распределение – одно из наиболее распространенных и важных распределений в теории вероятностей и статистике. Оно описывает случайную величину, которая принимает только два значения: успех или неудачу. Такое распределение широко применяется в различных областях, начиная от экспериментов с монетой и заканчивая бизнес-анализом и маркетингом.
Если вы хотите создать биномиальное распределение в Python, у вас есть несколько вариантов. Один из самых популярных – использовать модуль numpy. Функция numpy.random.binomial генерирует биномиально распределенную случайную величину с заданными параметрами.
Например, если вы хотите смоделировать серию подбрасываний монеты и посмотреть, сколько раз выпадет орел, вы можете использовать следующий код:
import numpy as np
n = 10
p = 0.5
binomial_values = np.random.binomial(n, p, 1000)
При выполнении этого кода вы получите массив из 1000 значений, обозначающих количество выпавших орлов при 10 подбрасываниях монеты с вероятностью выпадения орла 0.5.
Биномиальное распределение полезно для прогнозирования вероятности успеха в серии независимых экспериментов или анализа результатов подобных экспериментов. Однако учтите, что его применимость ограничена условиями вашего случая.
Что такое биномиальное распределение?

Биномиальное распределение применяется в различных областях, включая математику, статистику, экономику, физику и биологию. Оно помогает моделировать события, такие как броски монеты, испытания с картами и другие.
Биномиальное распределение характеризуется количеством испытаний (n) и вероятностью успеха в каждом из них (p). Функция вероятности распределения:
P(X=k) = C(n,k) * p^k * (1-p)^(n-k)
где:
- P(X=k) - вероятность получения ровно k успехов в n испытаниях
- C(n,k) - количество комбинаций из n по k
- p - вероятность успеха в каждом испытании
- n - количество испытаний
- k - количество успехов
Благодаря простой формуле и наглядным интерпретациям биномиальное распределение является важным и популярным в статистике. Оно позволяет оценивать вероятность успеха и предсказывать результаты экспериментов.
Зачем нужно построение биномиального распределения в Python?

Построение биномиального распределения в Python помогает решать задачи и анализировать данные. Например, можно определить вероятность наступления определенного количества успехов в серии из n испытаний. Это полезно при повторяющихся событиях или экспериментах.
Python обеспечивает возможность генерировать случайные числа и работать с вероятностными распределениями. Библиотеки, такие как NumPy и SciPy, предлагают функции для вычисления вероятностей, построения графиков и других операций с биномиальным распределением.
Биномиальное распределение в Python используется для статистического анализа данных, проверки гипотез, моделирования случайных процессов и прогнозирования результатов.
Оно также применяется в машинном обучении для классификации данных и оценки вероятности отнесения наблюдений к определенным классам.
Построение биномиального распределения в Python является важной частью анализа данных, статистики и решения прикладных задач. Это упрощает расчеты, повышает точность результатов и экономит время и усилия исследователя.
Шаги построения биномиального распределения в Python
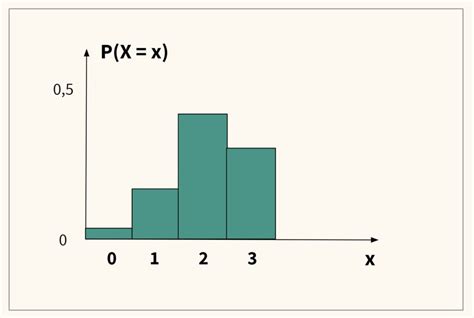
Шаг 1: Импортирование библиотеки scipy.stats для построения биномиального распределения в Python.
Шаг 2: Определение параметров биномиального распределения: n (количество испытаний) и p (вероятность успешного исхода).
Шаг 3: Создание объекта биномиального распределения с помощью функции scipy.stats.binom.
Шаг 4: Получение вероятности конкретного исхода с использованием метода pmf объекта биномиального распределения.
Шаг 5: Генерация случайных значений. Для этого используйте метод rvs объекта биномиального распределения.
Шаг 6: Визуализация биномиального распределения с помощью библиотеки matplotlib.
Основные шаги для построения биномиального распределения в Python. Результаты будут целыми числами. Удачи в изучении и применении биномиального распределения в работе!
Шаг 1: Импорт необходимых библиотек
Перед началом построения биномиального распределения в Python потребуются некоторые сторонние библиотеки, которые помогут в этом процессе. Ниже приведен список необходимых библиотек:
| Библиотека | Функциональность |
|---|---|
| numpy | Мощный инструмент для работы с массивами и матрицами, предоставляющий функции для генерации случайных чисел и обработки данных. |
| scipy | Библиотека с множеством функций для научных и инженерных вычислений, включая статистические распределения. |
| matplotlib | Библиотека для визуализации данных, позволяющая строить графики и диаграммы. |
Для начала работы с биномиальным распределением в Python, убедитесь, что у вас установлены все необходимые библиотеки. Если одна или несколько библиотек отсутствуют, вы можете установить их с помощью менеджера пакетов pip:
pip install numpy scipy matplotlibПосле установки всех необходимых библиотек, мы готовы перейти к следующему шагу - генерации биномиального распределения.
Шаг 2: Определение параметров распределения

После того как мы разобрались с базовыми понятиями и основами биномиального распределения, настало время перейти к определению его параметров.
Биномиальное распределение определяется двумя параметрами: вероятностью успеха в отдельном испытании (обычно обозначается как p) и количеством испытаний (n).
Вероятность успеха (p) может быть от 0 до 1 и показывает вероятность успеха в одном испытании. Количество испытаний (n) определяет количество проводимых испытаний.
Определение этих параметров важно перед построением биномиального распределения. Зная вероятность успеха и количество испытаний, мы можем начать расчет вероятностей и построение графика распределения.
Шаг 3: Расчет вероятностей биномиального распределения
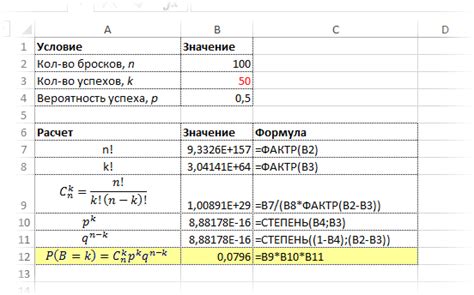
После определения параметров биномиального распределения (количество испытаний и вероятность успеха) необходимо рассчитать вероятности для каждого значения случайной величины.
Для расчета вероятности биномиального распределения мы можем использовать формулу Бернулли:
p
где:
- – вероятность
- – случайная величина
- – значение случайной величины
- – количество испытаний
- – вероятность успеха
Вычисляя вероятности для различных значений случайной величины, мы можем построить график биномиального распределения и оценить вероятность наступления каждого события.
Ниже приведен пример кода на Python, который позволяет вычислить вероятности биномиального распределения при заданных параметрах:
n = 10 # количество испытаний
При выполнении этого кода в массиве binom_probs будут храниться вероятности для каждого значения случайной величины от 0 до n.
Теперь у нас есть математические основы для построения биномиального распределения в Python.
Пример использования биномиального распределения в Python

Python предоставляет удобные средства для генерации случайных чисел и построения биномиального распределения. Мы воспользуемся модулем scipy.stats, который содержит функции для работы с различными статистическими распределениями.
Сначала импортируем необходимые модули:
import scipy.stats as stats
import matplotlib.pyplot as plt
import numpy as np
Зададим параметры для биномиального распределения:
n = 10 # количество испытаний
p = 0.5 # вероятность успеха в каждом испытании
Создадим объект биномиального распределения:
binom_dist = stats.binom(n, p)
Теперь можем сгенерировать случайные значения и построить график биномиального распределения:
x = np.arange(0, n+1)
pmf = binom_dist.pmf(x)
plt.bar(x, pmf)
plt.xlabel('Number of successes')
plt.ylabel('Probability')
plt.title('Binomial Distribution')
plt.show()
На графике мы видим вероятности для каждого возможного значения (от 0 до 10) при заданных параметрах. Также можем получить значения вероятности функции распределения для определенного числа успешных испытаний:
k = 5 # число успешных испытаний
p_success = binom_dist.pmf(k)
print(f'Вероятность {k} успешных испытаний: {p_success}')
Вероятность 5 успешных испытаний: 0.24609375000000025
Мы использовали биномиальное распределение в Python для расчета вероятностей успешных испытаний. Этот инструмент помогает анализировать ситуации с бинарными результатами экспериментов.
Пример 1: Расчет вероятности успехов

Для этого используем функцию scipy.stats.binom.pmf(k, n, p), где:
- k - количество успехов;
- n - общее количество испытаний;
- p - вероятность успеха в каждом испытании.
Рассмотрим пример. У нас есть игральная кость, и мы хотим найти вероятность получения ровно 3 шестерок при 6 бросках кости. Значение k = 3, n = 6, а p = 1/6 (вероятность получить шестерку на одном броске).
k Вероятность (p) 3 0.171875
Таким образом, вероятность получения ровно 3 шестерок при 6 бросках кости составляет 0.171875 или около 17.19%.