Геометрия изучается в 7 классе. Углы - одна из основных тем. Угол образуется двумя лучами, у которых общее начало - вершина угла. Каждый угол имеет градусную меру, которую можно найти с помощью простых формул и правил.
Один из способов найти градусную меру угла - использование тригонометрических функций. Например, при известных длинах сторон треугольника можно использовать теорему косинусов или теорему синусов для определения градусной меры угла. Эти теоремы основаны на соотношении сторон треугольника и угла между ними.
Существуют разные способы определения градусной меры угла. Например, прямой угол равен 90 градусам, а смежные углы в сумме дают 180 градусов. Эти простые правила помогают решать геометрические задачи.
Изучение градусной меры угла в 7 классе помогает развить у школьников абстрактное мышление, аналитические навыки и логическое мышление. Они смогут применять полученные знания в повседневной жизни. Знание градусной меры угла является важным для изучения геометрии и других математических предметов.
Как найти градусную меру угла в 7 классе
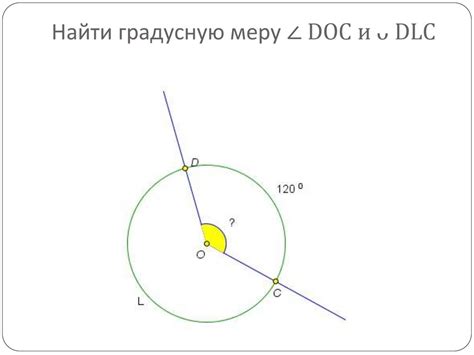
Градус – это единица измерения угла. Полный оборот – это 360 градусов. Половина оборота, или 180 градусов, соответствует прямому углу. Чтобы найти градусную меру угла, вам необходимо знать несколько правил и формул.
Правило 1: Сумма градусных мер двух смежных углов равна 180 градусам. Смежные углы это углы, у которых общая сторона и один конец совпадают.
- Например, если два угла являются смежными и их градусные меры равны, то каждый из этих углов равен 90 градусам (по половине оборота).
- Если один угол равен 60 градусам, то его смежный угол равен 120 градусам (180 - 60).
Правило 2: Сумма градусной меры угла и его внешнего угла равна 360 градусам. Внешний угол образуется при продолжении одной из сторон угла.
- Например, если угол равен 100 градусам, то его внешний угол равен 260 градусам (360 - 100).
Правило 3: Градусная мера угла может быть найдена с помощью гониометра – инструмента, специально предназначенного для измерения углов.
Зная эти правила и используя гониометр, вы сможете легко и точно найти градусную меру угла в 7 классе по геометрии.
Основные понятия в геометрии
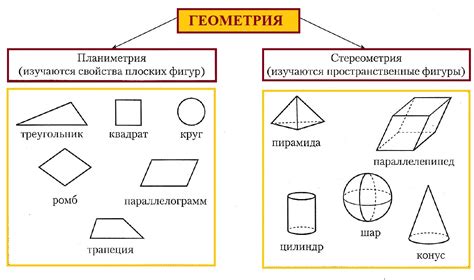
Угол – это фигура, образованная двумя лучами с общим началом. Начало угла называется вершиной, а лучи – сторонами угла. Угол измеряется в градусах.
Прямой угол – это угол, который равен 90 градусам. Он образуется двумя перпендикулярными линиями.
Острый угол – это угол, который меньше 90 градусов. Он образуется двумя лучами, которые встречаются внутри угла.
Тупой угол – это угол, который больше 90 градусов, но меньше 180 градусов. Он образуется двумя лучами, которые встречаются внутри угла.
Полный угол – это угол, который равен 180 градусам. Он образуется двумя противоположными направленными лучами.
Углы могут быть острыми, прямыми, тупыми, а также равными и разными по величине. Изучение углов и их свойств является одной из важнейших задач в геометрии.
С помощью градусного меридиана можно точно измерить угол, используя градусы, минуты и секунды. Градус – это основная единица измерения углов, равная 1/360 полного угла.
Познакомившись с основными понятиями в геометрии и научившись измерять углы в градусах, вы сможете легко решать задачи и проводить конструкции, связанные с углами в пространстве.
Углы и их свойства
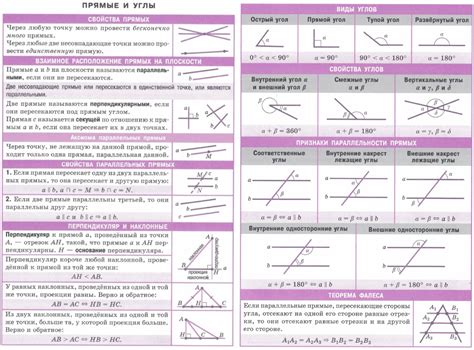
Основные понятия и свойства углов:
- Вершина угла - точка, где пересекаются два луча;
- Стороны угла - лучи, образующие угол;
- Мера угла - величина угла в градусах (°);
- Прямой угол - угол 90°;
- Острый угол - угол меньше 90°;
- Тупой угол - угол больше 90°;
- Смежные углы - углы с общей стороной и вершиной;
- Вертикальные углы - пара углов, образованных пересекающимися прямыми и равных между собой;
- Смежные и вертикальные углы в сумме равны 180°;
- Углы, дополняющие друг друга, в сумме равны 90°;
- Смежные и дополняющие углы образуют прямой угол.
Понимание основных понятий и свойств углов помогает решать геометрические задачи, находить неизвестные углы и указывать размеры углов в градусах. При решении задач важно уметь анализировать данные, использовать свойства углов и применять соответствующие формулы и методы решения.
Градусная мера угла
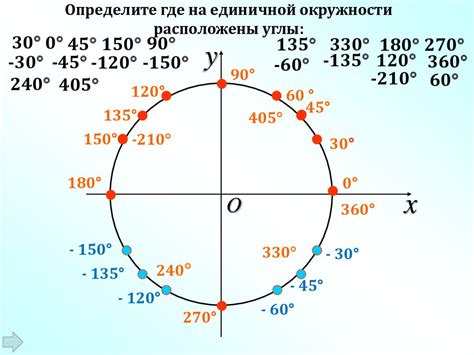
1 градус равен 1/360 части полной окружности. Полная окружность равна 360 градусам. Величина угла, меньшего полной окружности, измеряется в градусах.
Для измерения углов используется транспортир, инструмент, который помогает определить и отметить градусную меру угла. Транспортир состоит из полукруглой части, градусников и линейки.
Чтобы определить градусную меру угла с помощью транспортира, следует разместить его так, чтобы начало линейки совпало с вершиной угла, а середина или 0° транспортира совпали с первым лучом угла. Затем следует прочитать значение на градуснике транспортира, на котором находится второй луч угла.
Градусную меру угла можно представить в различных форматах. Например, 40° градусов или 40° градусов и 30 минут. Доли градуса, такие как минуты и секунды, позволяют более точно измерить углы.
Понимание градусной меры угла поможет решать разнообразные задачи, связанные с геометрией, строительством и другими областями науки. Умение измерять и работать с углами - важный навык, который пригодится в школе и в жизни.
Формула для нахождения градусной меры угла

Для нахождения градусного значения угла нужно знать его тип и иметь значения одного из его углов. В 7 классе по геометрии можно встретить три основных типа углов: прямой угол, острый угол и тупой угол.
Прямой угол имеет 90 градусов. Это половина от 180 градусов, которые составляют полный оборот. Прямой угол можно найти, зная значение одного из его углов и используя формулу:
| Тип угла | Формула |
|---|---|
| Прямой угол | 90° |
| Острый угол | Меньше 90° |
| Тупой угол | Больше 90°, но меньше 180° |
Например, если у нас есть треугольник ABC, и известно, что угол A равен 45 градусов, то угол C будет прямым углом, так как общая сумма углов треугольника равна 180 градусов. Таким образом, градусная мера угла C будет составлять 90 градусов.
У прямоугольника противоположные углы равны. Итак, угол ABD равен углу ADC. Сумма всех углов прямоугольника равна 360 градусов. Поэтому угол ABD + угол ADC = 360 градусов. Нам известно, что угол ADC равен 120 градусам. Подставим это значение в уравнение: угол ABD + 120 = 360. Упростим, получаем угол ABD = 360 - 120 = 240 градусов. Таким образом, градусная мера угла ABD равна 240 градусам.
| Прямоугольник ABCD имеет два параллельных противоположных стороны, поэтому его углы смежные и сонаправленные. Угол ABD смежный с углом ABC, который является прямым, то есть равен 90 градусам. Следовательно, градусная мера угла ABD также равна 90 градусам. |
Пример 3:
| Задача: | Даны две прямые AB и CD, пересекающиеся в точке O. Найдите градусную меру угла AOC, если градусная мера угла AOB равна 60 градусам. |
| Решение: | Углы, образованные пересекающимися прямыми, называются вертикальными. Так как угол AOB = 60 градусам, а угол AOC является вертикальным углом, то градусная мера угла AOC также равна 60 градусам. |
В 7 классе по геометрии важно знать, как найти градусную меру угла. Градусная мера зависит от вида угла и свойств фигур, на которых он определен. Зная эти свойства и используя формулы, можно решать задачи на нахождение градусной меры углов.
Практическое применение градусной меры угла

Градусная мера угла используется во многих областях, вот несколько примеров:
1. Строительство и архитектура
Градусы - основная система измерения для строительства и архитектуры. Они используются для определения углов наклона крыш, расположения стен и разметки объектов. Благодаря градусам строители и архитекторы могут определить размеры и углы конструкций для создания надежных и красивых строений.
2. Навигация
Градусы также применяются в навигации для определения направления движения. Компасы и навигационные инструменты помогают ориентироваться по курсу, используя градусы и направления. Моряки и путешественники используют градусы для определения местоположения островов или горизонта.
3. Ежедневные задачи
Градусы также применяются в повседневной жизни. Они помогают решать геометрические задачи, например, при измерении углов или оптимизации просмотра телевизора. Знание градусов помогает людям понимать пространственное расположение объектов.