Медиана - это основная мера центральной тенденции в статистике, которая делит упорядоченный ряд данных на две равные части. Нахождение медианы важно для анализа данных и применяется в экономике, социологии и медицине.
Чтобы найти медиану, нужно упорядочить данные и выбрать значение, которое находится посередине. Если количество данных четное, медиана будет средним из двух средних значений. Медиана не учитывает выбросы, в отличие от среднего значения.
Формула для нахождения медианы: Медиана = (n + 1) / 2, где n - количество данных.
Как найти медиану:
Для этого нужно:
- Упорядочить данные по возрастанию или убыванию.
- Если количество значений в выборке нечетное, то медиана будет средним значением. Найти значение, находящееся посередине упорядоченной выборки.
- Если количество значений в выборке четное, то медиана будет являться средним арифметическим двух значений, находящихся посередине упорядоченной выборки.
Например, для выборки (2, 4, 6, 8, 10), медиана будет равна 6, так как она разделяет выборку на две равные части (2, 4) и (8, 10).
Нахождение медианы важно при анализе статистических данных, так как она позволяет оценить центральную тенденцию выборки и сравнивать данные между собой.
Формула вычисления медианы
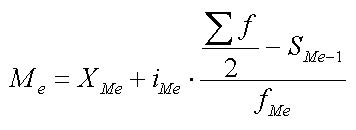
Формула вычисления медианы зависит от типа данных:
- Для нечётного числа значений: медиана равна значению в середине отсортированного набора данных.
- Для чётного числа значений: медиана равна среднему арифметическому двух значений в середине отсортированного набора данных.
Для вычисления медианы необходимо выполнить следующие шаги:
- Упорядочить набор данных в порядке возрастания или убывания.
- Определить размер набора данных (количество значений в нем).
- Проверить, является ли размер набора данных нечётным или чётным.
- Если размер набора данных нечётный, то медиана будет равна значению в середине.
- Если размер набора данных чётный, то медиана будет равна среднему арифметическому двух значений в середине.
Например, рассмотрим набор данных: 10, 20, 30, 40, 50.
- Упорядочим значения в порядке возрастания: 10, 20, 30, 40, 50.
- Размер набора данных равен 5.
- Размер набора данных нечётный, поэтому медиана будет равна значению в середине, то есть 30.
Таким образом, в данном случае медиана равна 30.
Статистика и ее связь с медианой

Связь между медианой и статистикой заключается в том, что медиана является одним из показателей, используемых в статистике для описания данных. Например, при анализе распределения доходов в стране, медиана позволяет нам определить, какой доход можно считать "средним" для большинства населения, не учитывая выбросы в данных.
В статистике также используется понятие "дисперсии", которая показывает, насколько разбросаны данные вокруг среднего значения. Медиана, в отличие от среднего значения, менее чувствительна к выбросам и аномалиям, что делает ее более надежным показателем в некоторых случаях.
Медиана - важный статистический показатель. Она помогает понять распределение данных и определить "среднюю" или "типичную" величину. Часто используется вместе с другими показателями, такими как среднее значение и дисперсия, для более полного представления информации.
Примеры использования медианы в анализе данных
Пример 1: Определение центрального значения выборки
Предположим, у нас есть выборка из 9 значений: 5, 3, 8, 6, 2, 9, 4, 7, 1. Чтобы найти центральное значение выборки, используем медиану. Медианой будет число, которое занимает среднее положение после упорядочивания выборки в порядке возрастания: 1, 2, 3, 4, 5, 6, 7, 8, 9. Таким образом, медиана равна 6.
Пример 2: Обработка выбросов
Предположим, что у нас есть выборка из 10 значений дохода сотрудников компании: 25000, 26000, 27000, 28000, 29000, 30000, 31000, 32000, 33000, 100000. Если мы рассчитаем среднее арифметическое, получим значение около 36500, что не является репрезентативным для большинства сотрудников. В этом случае медиана может быть предпочтительнее, так как она не чувствительна к выбросам. После упорядочивания значений, медиана равна 30000.
Пример 3: Ранжирование данных
| 2. Если количество данных нечетное, медиана будет значением, находящимся посередине. Например, в последовательности 1, 2, 3, 4, 5 медианой будет 3. |
| 3. Если количество данных четное, медиана будет средним арифметическим двух значений, находящихся посередине. Например, в последовательности 1, 2, 3, 4 медианой будет (2 + 3) / 2 = 2.5. |
Эти правила позволяют определить медиану для любого набора числовых данных. Медиана является более устойчивым показателем по сравнению с средним арифметическим, поскольку она не зависит от наличия экстремальных значений и склонна лучше отражать типичное значение в выборке данных.
Медиана и выбросы в статистике

Иногда выборка содержит выбросы - экстремальные значения, которые значительно отличаются от остальных данных. Эти значения могут быть вызваны ошибками измерений, аномалиями или другими причинами.
Выбросы могут существенно повлиять на расчет медианы. Если выборка содержит выбросы, то значение медианы может значительно отличаться от "обычного" значения в выборке. Это может привести к искажению результатов и неправильной интерпретации данных.
Для определения наличия выбросов в выборке и их влияния на медиану можно использовать различные методы, например, построение "ящика с усами" с помощью диаграммы размаха или анализ значения выбросов относительно медианы и других статистических показателей.
Если выборка содержит выбросы и их влияние на медиану существенно, может быть целесообразно использовать другой показатель центральной тенденции, например, среднее значение или моду.
| Выборка без выбросов | Выборка с выбросами |
|---|---|
| 1, 2, 3, 4, 5 | 1, 2, 3, 4, 100 |
| Медиана: 3 | Медиана: 3 |
Значение медианы в прикладных областях

В медицине медиана часто используется для определения типичного значения параметра в выборке. Например, при изучении запаса дыхательных объемов у пациентов с определенным заболеванием, медиана может показать, какое значение объема является типичным для большинства пациентов из выборки.
Медиана используется в экономике для анализа распределения доходов или стоимости товаров. Например, медианное значение дохода позволяет оценить уровень жизни или социальной дифференциации в группе населения.
В социологии и психологии медиана помогает изучать распределение характеристик в обществе или группе людей. Например, медиана возраста помогает определить типичную возрастную группу в популяции.
Использование медианы в различных областях позволяет более точно анализировать данные, учитывая выбросы и асимметрию распределения. Она отражает центральную тенденцию выборки и может быть более репрезентативной в некоторых случаях, чем среднее значение.